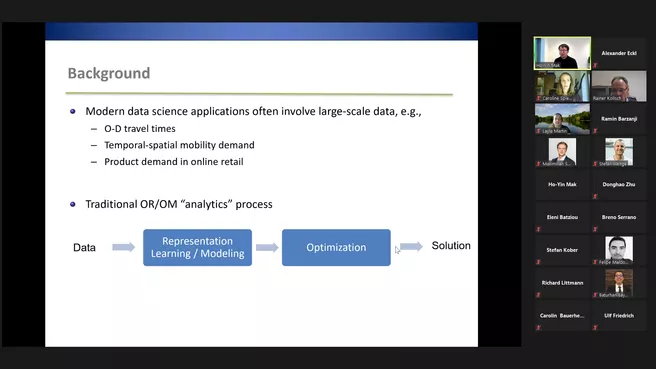
Prof. Ho-Yin Mak (University of Oxford): Dimensionality Reduction for Stochastic Optimization – Modern data science applications often involve high-dimensional data. A common approach involves first performing dimensionality reduction on the data, and then subsequently solving the optimization problem with the low-dimensional representation. However, standard dimensionality reduction methods are designed to maximize the amount of information retained in the representation, which do not generally reflect performance in the subsequent optimization task (i.e., the importance of such information in the optimization problem).
In this work, we aim to develop an alternative dimensionality reduction method that minimizes the degree of suboptimality in the optimization phase. We show that this can be done via solving a distributionally-robust optimization problem, which admits a semidefinite programming relaxation. We shall discuss some computational results based on a vehicle repositioning problem.
This is a joint work with Long He (National University of Singapore).