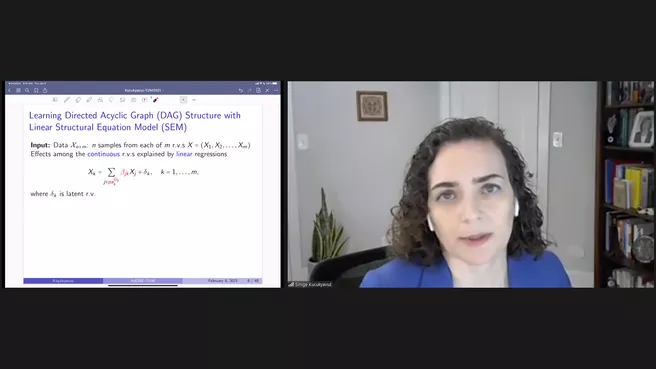
Prof. Simge Küçükyavuz (Northwestern University): Mixed-Integer Convex Programming for Statistical Learning – In the first part of this talk, we consider the problem of learning an optimal directed acyclic graph (DAG) from continuous observational data. We cast this problem in the form of a mathematical programming model which can naturally incorporate a super-structure to reduce the set of candidate DAGs. We use the penalized negative log-likelihood score function with both L0 and L1 regularizations and propose a mixed-integer quadratic program (MIQP), referred to as a layered network (LN) formulation. The LN formulation is a compact model, which enjoys as tight an optimal continuous relaxation value as the stronger but larger formulations under a mild condition. Computational results indicate that the proposed formulation outperforms existing mathematical formulations and scales better than available algorithms that can solve the same problem with only L1 regularization. In particular, the LN formulation clearly outperforms existing methods in terms of computational time needed to find an optimal DAG in the presence of a sparse super-structure.
This is joint work with H. Manzour, A. Shojaie, L. Wei and H-H. Wu.
Motivated by related statistical learning problems, in the second part of this talk, we present the convexification of a class of convex optimization problems with indicator variables and combinatorial constraints on the indicators. Specifically, we give the convex hull description of the epigraph of the composition of a one-dimensional convex function and an affine function under arbitrary combinatorial constraints.
This is joint work with A. Gómez and L. Wei.